Appendix
- 26.09.2013
- Lesezeit ca. 2 min
Das Modell im Detail
Die Messung der versteckten Arbeitslosenrate beruht auf einem Modell das erstmals von Perry (1971) erwähnt und später unter anderem von Zweimüller (1990), Mitchell (2007) und Agbola (2005) in ähnlicher Weise angewendet wurde.
In der Fachliteratur sind prinzipiell zwei Methoden zur statistischen Berechnung von versteckter Arbeitslosigkeit vorgesehen. Die Trendextrapolation schätzt mittels einer Regression die Erwerbsquote bei Vollbeschäftigung[1]. Diese Methode liefert oft verzerrte Ergebnisse. Daher wird hier ein Modell verwendet, das die Erwerbsquote mithilfe einer Konjunkturvariable schätzt. Als Konjunkturvariable wird wie bei Zweimüller (1990), Mitchell (1999) und Agbola (2005) die Beschäftigungsquote gewählt. Fuchs (2002) erwähnt, dass man auch andere Konjunkturvariablen heranziehen kann[2].
Die Möglichkeit, diese Schätzung geschlechtsspezifisch und für einzelne Altersgruppen durchzuführen, führt zu folgendem ökonometrischen Modell:
Hier beschreibt EQi die Erwerbsquote der Bevölkerungsgruppe i (= Erwerbspersoneni/Bevölkerung); BQ die Beschäftigungsquote der gesamten arbeitsfähigen Bevölkerung (= Beschäftigte/Bevölkerung); PQi die Bevölkerungsquote der demographischen Gruppe i (= Bevölkerungi/Bevölkerung); ∆t die Veränderung der Variablen zum Zeitpunkt t; α, β, γ die Regressionsparameter; und εi,t das Residuum. Der Koeffizient α spiegelt die konjunktur- und demografieunabhängige Komponente der Veränderung der Erwerbsquote wider (e.g. unterschiedliche Präferenzen). β misst die Konjunkturreagibilität der Erwerbsquote (Veränderung der Erwerbsquote der Gruppe i – aufgrund einer Veränderung der Beschäftigungsquote um einen Prozentpunkt). Die Bevölkerungsquote dient als Kontrollvariable, γ misst die Veränderung der Erwerbsquote (der Gruppe i) bei einer Veränderung der Bevölkerungsquote (der Bevölkerungsgruppe i) um einen Prozentpunkt.
Daraus wird die versteckte Arbeitslosenquote (VALQ) berechnet. Die versteckte Arbeitslosenquote misst die zusätzliche Erwerbsquote im Falle einer Wirtschaft mit Vollbeschäftigung:
VALQi (= Versteckte Arbeitslosei/Bevölkerung) ist die versteckte Arbeitslosenquote und BQ* der Hochkonjunkturwert der Beschäftigungsquote. Diese Methode liefert zuverlässige Ergebnisse, weil die starken Schwankungen der Erwerbsquote über einen gewissen Zeitraum erfasst werden. Die Berechnung des BQ* basiert auf Mitchell (1999).
Für die Vollbeschäftigung gilt:
L* ist das Arbeitskräftepotenzial, L sind die aktuellen Erwerbspersonen und VAL sind die versteckten Arbeitslosen. Unter Zuhilfenahme der Definition der versteckte Arbeitslosenquote und Gleichung (2), kann die versteckte Arbeitslosenquote geschrieben werden als:
N* stellt die Vollbeschäftigung und N die aktuelle Beschäftigung dar. Nehmen wir x* als die Arbeitslosenrate bei Vollbeschäftigung:
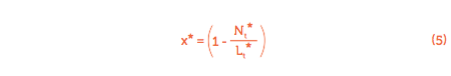
dann kann mithilfe dieser Definition, Gleichung (3) und Gleichung (4), die Vollbeschäftigung N* geschrieben werden als:
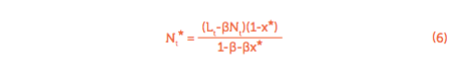
Die Zahl der versteckten Arbeitslosen für die Bevölkerungsgruppe i berechnet man als Produkt der versteckten Arbeitslosenquote und der gesamten Bevölkerung (B):
Regressionsergebnisse:
In diesem Kapitel werden die Regressionsergebnisse im Detail für Österreich (Männer und Frauen), Deutschland, Schweden, Finnland und Großbritannien (UK) gezeigt. Die Regression wird mittels OLS-Methode und mit heteroskedastiekonsistenten (robusten) Standardfehlern geschätzt (White correction). Hinweise auf ein Multikollinearitätsproblem gibt es nicht, da die beiden erklärenden Variablen nur eine sehr schwache Korrelation aufweisen.
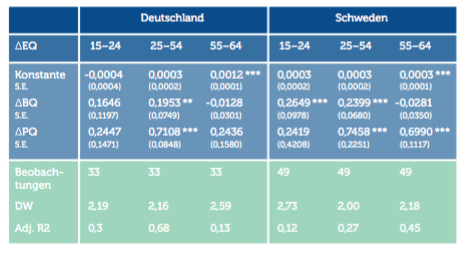
Die Ergebnisse für Männer und Frauen in Österreich sind in den Altersgruppen 25 bis 54 und 55 bis 64 signifikant. Für die 15- bis 24-Jährigen sind die Ergebnisse statistisch nicht signifikant. Die mögliche Autokorrelation (hoher Wert der DW-Statistik) bei Männern zwischen 55 und 64 ist auf einen Ausreißer am Anfang der Beobachtungsperiode zurückzuführen. Würde man den Ausreißer (der eventuell mit der Wahl 1999 zusammenhängen könnte) herausnehmen, läge der Wert der DW-Statistik bei 2,06 und wäre somit nicht problematisch. Der β-Koeffizient würde sich nur minimal verändern. Für Deutschland[3] und Schweden erhalten wir ebenso gute Ergebnisse. Die β-Schätzer sind zum Großteil signifikant, lediglich in der alten Generation sind sie es nicht. In Finnland und Großbritannien sind β-Schätzer für alle Altersgruppen signifikant. Auch hier sind die Testergebnisse durchaus zufriedenstellend.
β-Schätzer im Ländervergleich
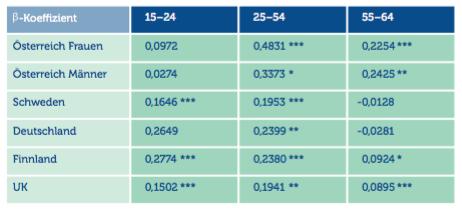
Tabelle 4. Quelle: Agenda Autria.
Österreich weist zwar in der Gruppe der Jüngeren die niedrigsten β-Koeffizienten auf. In der Gruppe der 25- bis 54-Jährigen und auch in der Gruppe der 55- bis 64-Jährigen sind diese jedoch um einiges höher als in den Vergleichsländern. Zweimüller (1990) zeigt, dass diese β-Koeffizienten bis 1985 in der Altersgruppe der Jungen am höchsten waren. Offensichtlich hat sich seit damals strukturell einiges in Österreich verändert. Die Frühpensionierungsproblematik scheint also ein eher „modernes“ Phänomen zu sein.
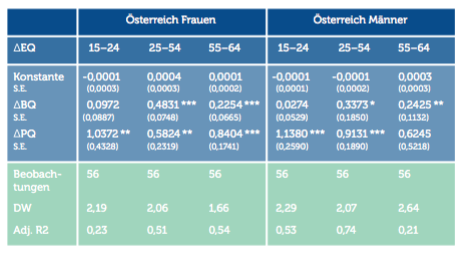
Anmerkungen: Alle Regressionen werden mittels OLS-Methode mit heteroskedastiekonsistenten (robusten) Standardfehlern geschätzt (White correction). Standardabweichungen in Klammern (S.E.).
DW – Durbin-Watson Statistik für Autokorrelation.
Die mögliche Autokorrelation bei Männern zwischen 55 und 64 in Österreich ist auf einen Ausreißer am Anfang der Beobachtungsperiode zurückzuführen. Würde man den Ausreißer (der eventuell mit der Wahl 1999 zusammenhängen könnte) herausnehmen, läge der Wert der DW-Statistik bei 2,06.
Adj. R2 – Lineares einfaches Bestimmtheitsmaß, angepasst nach Freiheitsgraden.
* Signifikant auf dem 10%-Level; ** Signifikant auf dem 5%-Level; *** Signifikant auf dem 1%-Level.
Anmerkungen: Alle Regressionen werden mittels OLS-Methode mit heteroskedastiekonsistenten (robusten) Standardfehlern geschätzt (White correction). Standardabweichungen in Klammern (S.E.).
DW – Durbin-Watson Statistik für Autokorrelation.
Adj. R2 – Lineares einfaches Bestimmtheitsmaß, angepasst nach Freiheitsgraden.
* Signifikant auf dem 10%-Level; ** Signifikant auf dem 5%-Level; *** Signifikant auf dem 1%-Level.
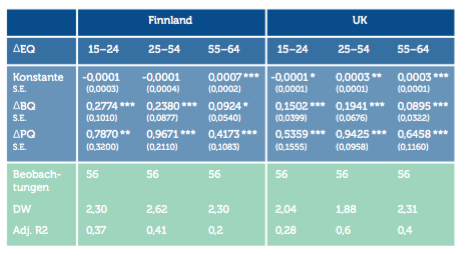
Anmerkungen: Alle Regressionen werden mittels OLS-Methode mit heteroskedastiekonsistenten (robusten) Standardfehlern geschätzt (White correction). Standardabweichungen in Klammern (S.E.).
DW – Durbin-Watson Statistik für Autokorrelation.
Adj. R2 – Lineares einfaches Bestimmtheitsmaß, angepasst nach Freiheitsgraden.
* Signifikant auf dem 10%-Level; ** Signifikant auf dem 5%-Level; *** Signifikant auf dem 1%-Level.
Fußnoten
- In dieser Regression werden ein geschätzter Trend und das Vollbeschäftigungsniveau kombiniert. Siehe auch Gordon (1972). ↩
- Z. B. die Arbeitslosenrate (-), die „Teilzeitarbeitslosenquote “ (-) oder die Relation „Offene Stelle zu abhängige Erwerbspersonen“ (+) . ↩
- Für Deutschland ist der Datensatz kürzer (von 2005:Q1), es gibt aber keine Hinweise auf Strukturbrüche im Zeitraum von 1999:Q1 bis 2013:Q1. ↩
Mehr interessante Themen
Der schnellste Weg aus der Budgetkrise
Die Staatsschulden sind rasant gestiegen, das Defizit wächst. Österreich muss rasch Maßnahmen setzen, um das Budget zu sanieren. Aber wie soll das gehen, ohne die Wirtschaftskrise zu verschärfen? Die Agenda Austria hat ein Konzept erarbeitet, mit dem der Staat schon im kommenden Jahr knapp 11 Milliarden Euro einsparen kann. Bis zum Ende des Jah
Verloren im Papierdschungel: Die erdrückende Last der Bürokratie
Fast schon im Wochentakt schlagen bei den Unternehmen neue Regeln auf. Es kann schon längst nicht mehr als EU-Bashing gelten, den Regelungswahn der Brüsseler Schreibtischakrobaten als unmäßig zu kritisieren. Wir werfen einen Blick in die Giftküche der Bürokratie.
Einschätzung der Wahlprogramme zur Nationalratswahl 2024
Schwerpunkt 1: Mehr Wachstum braucht das Land! Wirtschaftswachstum ist in Österreich zu einem Fremdwort geworden. Nicht nur in der Statistik und in den Prognosen der Institute ist es inzwischen weitgehend der Stagnation gewichen. Auch in den Wahlprogrammen der Parteien kommt es kaum noch vor. Man sollte ja erwarten, dass ein Land, dessen reales Br
Wie wir die Wohnungsnot lösen
Wohnen ist in Österreich nicht teurer als in anderen europäischen Ländern. Die Wohnkostenbelastung liegt unter dem EU-Schnitt. Und doch gibt es Verbesserungsbedarf: Künftige Regierungen sollten den Aufbau von Wohneigentum in der Mitte der Gesellschaft erleichtern, den geförderten Mietmarkt treffsicherer machen und dafür sorgen, dass ausreiche
Wie wir das Sozialsystem finanzierbar halten
Der Sozialstaat ist eine Errungenschaft, um die uns viele Menschen auf der Welt beneiden – aber auch eine finanzielle Belastung, die sich immer schwerer stemmen lässt. Die nächste Regierung wird um Sparmaßnahmen nicht herumkommen, wenn das System zukunftsfit bleiben soll. Für die Bürger muss das nicht unbedingt Verschlechterungen mit sich br
Eine Ausgabenschranke für den Staatshaushalt
Eigentlich wollte die Regierung ja die Staatsschulden senken und die Bürger entlasten. Beides ist leider spektakulär misslungen. In der kommenden Legislaturperiode muss die Politik das Ruder herumreißen und einen Sparkurs einschlagen. Die gute Nachricht: Es gibt ziemlich viele Maßnahmen, die man setzen kann.